
Neural ordinary differential equations
This paper received the best paper award at NeurIPS 2018.
Authors. Ricky T.Q. Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud
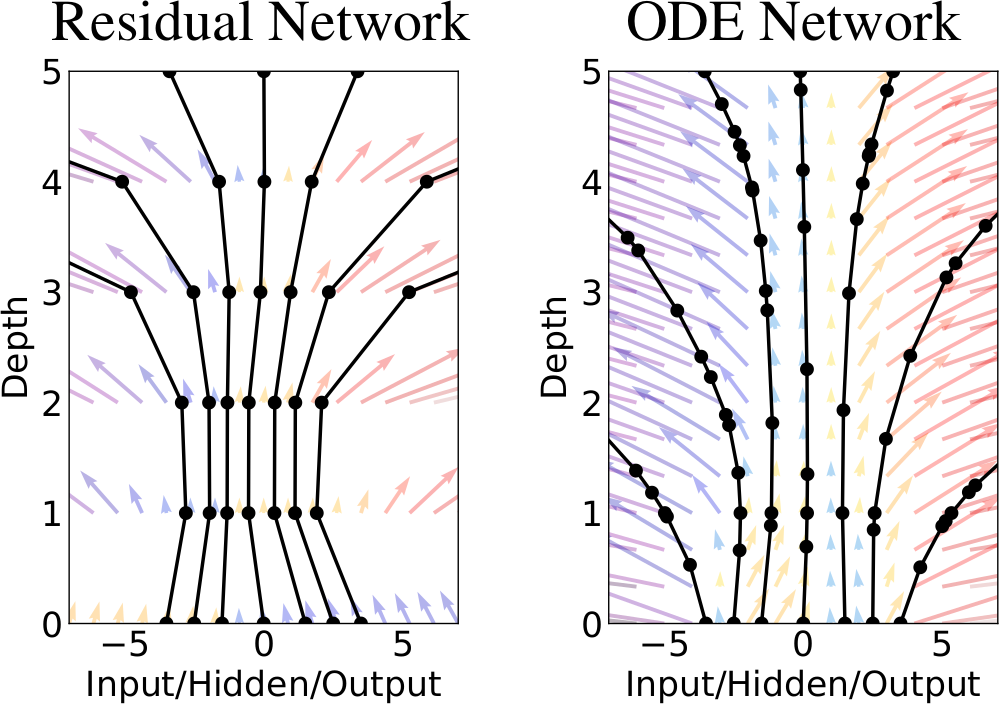
Abstract. In 2015, He, et.al. proposed the Residual networks. A simple modification to standard convolutional neural networks that made it possible to train a network of a much larger depth than before, and improved the performance of image classification (which was already impressive at the time). The idea behind residual networks is that each layer learns to model the difference between its input vector and its required output vector. This allows for gradients to propagate through deeper networks, and the transformations performed at each layer could thus be made smaller. Taking this to the limit, when the step taken in each layer goes towards zero (and the number of layers goes towards infinity), the update rule starts to resemble Euler's method for solving ordinary differential equations. In the paper Neural Ordinary Differential Equations by Ricky Chen, et.al., a true continuous depth neural network model is proposed based on solvers for ordinary differential equations. This leads to a number of benefits, such as a memory footprint that is independent of the depth of the model, and the ability of making a tradeoff between running time and precision at test-time.
Video capture of presentation.
Learning machines seminars at Research institutes of Sweden, 2019-01-31
Olof Mogren