
Augmented neural ODEs
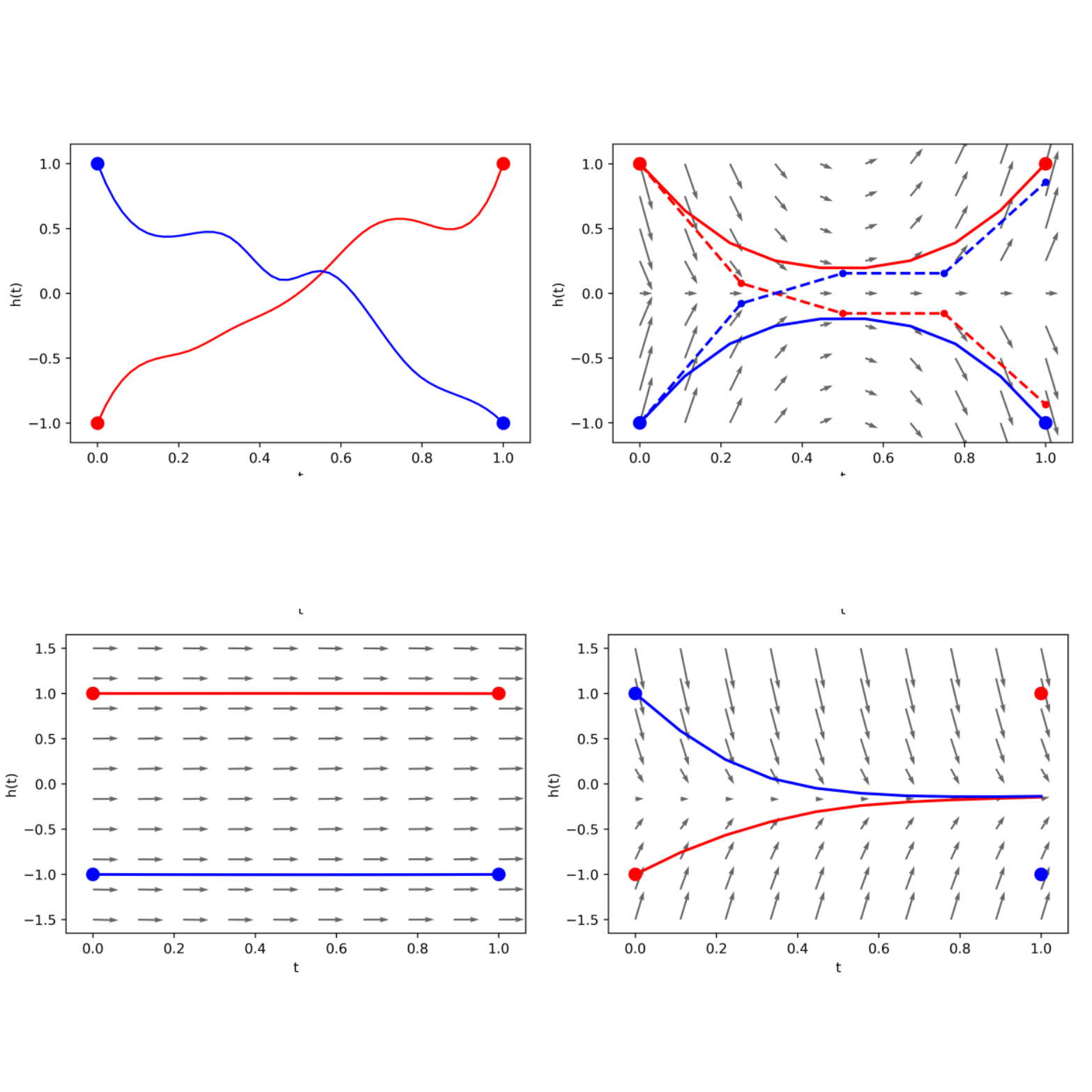
We show that Neural Ordinary Differential Equations (ODEs) learn representations that preserve the topology of the input space and prove that this implies the existence of functions Neural ODEs cannot represent. To address these limitations, we introduce Augmented Neural ODEs which, in addition to being more expressive models, are empirically more stable, generalize better and have a lower computational cost than Neural ODEs. https://papers.nips.cc/paper/8577-augmented-neural-odes
RISE Learning Machines Seminars, 2019-12-12
Olof Mogren